Learning science progresses funeral by funeral

So said one of the founders quantum mechanics Max Planck. But I think this quote applies to other areas of human endeavour as well. I have been working in the area of learning for major part of my adult life. During my own learning, when computers were just getting mainstream (late 1990s and early 2000s) I experienced first-hand how learning experience can be enhanced by proper use of computers. Another aspect of proliferation of computer which are connected to the internet is that you have access to sum of almost all human knowledge available to you. Even 20 years back this was not the case. I remember when I discovered that there are accessible resources about physics on the web, it was almost a revelation. And the resources grow day-by-day, becoming more and more accessible to everyone. Even with a smartphone you can access all the information on the web. Most modern web designers are adopting a mobile first policy.

I have been musing about these impacts on learning experience ever since. But there is a strong opposition to use technology in the classroom. This mostly comes from people in two categories. One is a old lot who grew and learned in a world without accessible technology and other is a younger lot who have weird (read extremist) ideas about teaching and learning. The younger lot is a lost tribe who live on the Eastern pole. Both these two categories of people opposed to use of technology in the classroom think that they are “progressive” and are fighting against “oppressive” technology.

A note on the term “technology”: Here I am using the term “technology” in a narrow sense of computer technology. A more inclusive sense would include blackboards, printed textbooks and the classroom itself as forms of technology.

I will try to present this perspective of opposition to technology in classroom and dismantle them giving a rebuttal. In some cases, the holders of these ideas are beyond redemption, and quote of the Max Planck which is the title of the post applies to them. They will die off and their technophobia will die with them. A newer generation of pedagogues conversant and comfortable with technology will emerge in the next generation and will be in tune with the need of the time.

Let us start with the older lot. Many of the progressive pedagogues grew in India that was deprived of any computer technology. This was the era of many socialist inspired people’s movement which aspired for egalitarian approach to education, particularly the sections of society which are low in socio-economic order. The approach was to enlighten the masses inspired from the socialist ideas. Now till 90s, the computer technology was expensive and its use even in the developed countries was rather limited. And most of the people in the older lot I am talking about did spend their formative and working years in this era.

Now it is not to say that all of the people did not have any contact with computers at all. Some of these inspired people were highly qualified individuals who did their research work in some of the best institutions in the world. Some of them had some experience of using the computers. But computers were never a second nature to them, as they are not to many people even now. And a lot of them never used computer, because in their era it was an expensive technology and hence they didn’t have access to it. Hence it made computer technology an alien artefact for them in that era.

And when computers finally became accessible, their own years of learning new things had long gone by. Some of them did adopt newer computer technology, able to see the potential to transform both learning and dissemination of knowledge, but most didn’t. Apart from the ideological commitment to a “non-computer” approach to learning, I think their own fears and phobia of being unable to learn and use the new technology also played a role in their opposition. This was the situation in early 2000s, which was still acceptable as computer and internet penetration was not good. These pedagogues threw anything to do with computers as too Western (hence sitting on Eastern pole from where every direction is West).

But by 2010, smart phones were becoming more and more common as were the desktop computers and laptops. By 2015, the access to cheap smart phones with fast internet exploded. Now, here were are in the mid 2020s when proliferation of computer devices in the form of smartphones, tablets and laptops is increasing by the day. The dreams of last mile connectivity are not far off.

The Covid-19 pandemic forced us to shift to online classes. Of course, it did have its issues particularly for students who lacked infrastructure in terms of devices and connectivity. But it did show that even with present conditions something is still possible. Yet, people had their doubts. Now its been

Yet, the resistance from the older pedagogues continues. They cannot get away from ideas about computers that were formed 4 decades back, when computers were still primitive and expensive. And they continue to the same arguments even today. Questions like “Have computers reached everyone?” and since they have not we cannot use them. Or they give overarching statements like “The most downtrodden will be neglected in this”. They are like classical physicists who could not accept ideas of modern physics at the turn of the last century.

To objections like these, I have two rebuttals, one is historical-pedagogical and other is on the nature of computer technology in particular. Let us look at the first objection: “Have computers reached everyone?”, of course, they have not! But what about other technologies like the classroom and blackboard? Yes they are technologies! Have they reached everyone? Of course not! But then you don’t give the same arguments, let school reach every child (or every child reach the school) and only then we will allow/accept school as a viable mechanism for learning. And that is something they will never accept, just because they are comfortable/conversant with technology school-classroom-black-board-textbooks. That is a given for them. But even that “technology” has access issues, and comes loaded with challenges of its own for learning. I mean these are the very challenges that many of these pedagogically oriented movements addressed.

So this argument about last-mile connectivity applies to the existing technologies to teaching and learning as well. Why should it be singled out for “computer” technology? This is only because the older lot is not familiar (rather don’t want to accept) with the potential of the computer technology as it would destroy their anachronistic cherished notions of teaching and learning.

Other major assumption in this notion is that the teacher and textbook are the (sometimes the only) source of knowledge, almost an axiom in the Euclidean sense.

Is this why there was so much focus on developing text-based teaching learning materials. But this is no longer true. We now have almost entire sum of human knowledge accessible literally at fingertips to anyone with a connected device. But now with Open Education and internet this is being challenged in a serious way. Added to this is the absolutely disruptive technology of AI bots like chatGPT. Why should learning be limited to a centralised textbook which usually does not take into account the context of learners written by folks sitting in ivory towers, which is not updated for years?

Now we have the technology and appropriate legal licenses to change this by really empowering learners to bypass the filters of textbooks and teachers. But still we are hung on cherished notion of teacher in the constructivist classroom.

Now, I come to aspects of the nature of technology and young learners. The nature of “computer” technology is such that younger learners adapt to it very quickly. They are still in the phase of learning about the world. A very young child given a smartphone will try out everything and figure out how it works (or doesn’t) and start playing with it as if its any other toy. Parents often ask help from their very young children to solve technological challenges they face.

Same is true for teachers. I have seen enough examples during my field work in very rural areas. Learners when exposed to computer technology even for a very short time several were first-generation learners who were using computer for the first time, could out-pace the teacher in using the computer for the task at hand. Now in the traditional approach (even the progressive ones) the knowledge of teacher is almost never surpassed in a teaching-learning setting. The teacher is always the “more-able-peer” in the Vygotskian sense and is considered as an a priori truth. Now, I am not denying that in many senses this is correct, but if you give access to technology to young learners in many cases the need for teacher is bypassed. This is in the true sense that a child constructs knowledge with the only difference being that it is not mediated by the teacher (or even if it is teacher is exactly a mediator). Constructionist microworlds provide excellent examples of such learning by the learners on their own. By denying access to computer technology, this is what is being missed.

Of course there are examples and examples of bad use of technology in the form of PPT/click books etc which is often rightfully criticised. But that is missing forest of the trees. Another point in this regard is that educational technology abhors vacuum, if any technology is not opted by good pedagogy, it will be co-opted by a bad one. So we need to stake claim, otherwise poor pedagogical approaches which just replicate what is done without a computer to be done on a computer. To give Papert’s analogy it would be like attaching a jet engine to a horse-wagon!

Now we come to the younger lot. They typically have grown with technology in their formative years. And as reasearchers and activists they use computers and internet and are familiar with the technologies. Yet they give the same arguments of “oppression” as the older lot. I mean it doesn’t occur to them they are using the same computers for their own work because it suits them. But when it comes to use in the classroom it is not to be used. Double standards much. If they think the computers are oppressive as much, they should stop using it themselves. But then how will they post social media updates on Facebook and Twitter?

The younger generation of people who oppose technology in the classroom fits very well in the category of people without skin in the game (after Taleb). For things they think computer is useful for themselves, they will make full use of it be it data analysis, report writing or other work. But they are not ready to give same concession to children (especially in resource deprived areas) who need such scaffolding more. Instead they want to deprive the children of a learning companion because it does not work with their ideological world view centred at Eastern pole. And some of these same researchers, when it comes to their own children will provide them with computers and tablets for learning. But when it comes to the children who need it more…

I could go on and on.. But you get the point, the opposition is not based on factual aspects but ideological and there too they are on thin ice. But the opposition is waning funeral by funeral and computers are the new normal…

August 26, 2024 The Mitr

Book Review: Parasite Rex by Carl Zimmer

This is a scary book. I mean it is a very good introduction to how parasites live their life among their hosts and thrive. The book takes look at various parasites and their natural history in terms of evolution and the impact parasites have in the ecology and individuals. How many behaviours in their hosts are manifestation of parasites trying to maximise their chances of getting too they next guy in their life cycles. For example, the malarial parasite plasmodium generates chemical signals that give us fevers at very specific times of the day which coincides with the time when mosquitos are active. From evading the immune system to completely controlling organisms by taking over their nervous system parasites are highly evolved in their way of life.

Zimmer takes a perspective that parasites have a major role in any functional ecosystem and drives the evolution of their hosts as well. Earlier parasites were treated as
Low end ke forms but studies now show his little we know how they work. Almost all wild animals are full of parasites and Zimmer also makes a case that having parasites is a sign of a good ecosystem. They are not organisms in the fringes but rather a driving force across the ecological niches.

Why I said the book is scary is the sheet amount of parasites that can easily enter your body and how little we can do about it. As you read about various ways in which you can get infected leaves you scared.

June 15, 2024 The Mitr

Illustrations for Alice in Wonderland – Part 3 – Peter Newell

Peter Newell was a prolific American illustrator and author. The books with his illustrations for Alice’s Adventures in Wonderland and Through The Looking Glass were published circa 1901. These are paintings rather than line drawings. The books were printed in black and white/grayscale so are the illustrations. But there must be a set of fully colour versions of these paintings. Some of them you can see here and there on the interwebs, but a complete collection I could not find. If you know of colour versions of these paintings please let me know.

Alice’s Adventures in Wonderland

Down she came upon a heap of dry leaves.

The poor little thing sat down and cried.

“Now I’m opening out like the largest telescope that ever was!”

The Rabbit started violently.

The Mouse gave a sudden leap out of the water.

The Caucus-Race.

The Dod solemnly presented the thimble.

“Mine is a long and a sad tale,” said the Mouse.

On various pretexts they all moved off.

“Why, Mary Ann, what are you doing here?”

“What’s that in the window?”

“Catch him, you by the hedge.”

The poor little Lizard Bill was in the middle being held up.

The Puppy jumped into the air.

The Caterpillar and Alice looked at each other.

Old Father William standing on his head.

Old Father William balancing an Eel on the end of his nose.

Old Father William turning a back somersault in at the door.

“Serpent!” screamed the Pigeon.

Then they both bowed low and their curls got entangled.

Singing a sort of lullaby.

Sp she set the little creature down.

This time it vanished quite slowly.

He dipped it into his cup of tea and looked at it again.

They lived at the bottom of a well.

Don’t go splashing paint over me.

“Off with her head!”

It would twist itself round and look up in her face.

“Don’t look at me like that.”

The Hedge-hog was engaged in a fight with another Hedge-hog.

“Tut, tut, child!” said the Duchess.

They began solemnly dancing round and round Alice.

“Will you walk a little faster,” said a Whitling to a Snail.

Alice began telling them her adventures.

“Come on!” cried the Gryphon.

June 11, 2024 The Mitr

Illustrations for Alice in Wonderland – Part 2 – John Tenniel

John Tenniel

John Tenniel’s illustrations are by far the most popular drawings for Alice. Over the years from their first publication in for Wonderland (1865) and Looking Glass (1871), these illustrations have had a life of their own.The original illustrations are line drawings, closely following Lewis Carroll’s illustrations in spirit and sometimes in framing also. Tenniel’s illustrations have had a very strong impact on all the later illustrations by other artists as well. His depictions of certain characters, at least for me, is intimately tied with the words of Lewis Carroll. I cannot imagine the story without reference to his illustrations.

Tenniel’s monogram of his stylised initials are part of all the illustrations.

Several later renditions of these were coloured or supplemented by full colour plates by other artists. We will make a separate post for these modified colour illustrations later. In this post we will see only the original illustrations as they appear in the 1865 edition a total of 42 including the front piece.

Over the years I have used several of these images in my presentation and work.

All images in public domain unless mentioned otherwise.

Front piece: the court of the king and queen of hearts.

The White rabbit.

Alice finds the little door.

Drink me! said the label on the bottle.

Alice becomes enlarged.

The white rabbit runs away.

Alice in pool of tears.

The mouse swims away.

The Dodo presents Alice a thimble.

The mouse’s long and sad tale.

Alice went on growing and growing till she filled the room.

Alice tries to snatch the rabbit from the window.

Alice kicks Bill the green lizard from the chimney.

Alice throws a stick to the giant puppy to fetch.

Alice meets the caterpillar.

Old Father William stands on his head.

Old Father William does a back-somersault.

Old Father William finishes the goose, with the bones and the beak.

Old Father William balances an eel on his nose.

The fish-footman delivers the invitation from the Queen to play croquet.

Alice meets Duchess and the crying baby.

The baby turns to a pig!

Alice meets the Cheshire cat.

Cheshire cat fades away. “ Well! I’ve often seen a cat without a grin,” thought Alice, “ but a grin without acat! It’s the most curious thing I ever saw in all my life.

At the mad tea party.

The Mad Hatter.

The Mad Hatter and the White Rabbit put the dormouse into the soup.

Colouring the white roses red.

Alice meets the queen and “Off with her head!” she commands.

Alice playing croquet with the flamingo and hedgehog.

“Off with his head” queen said for Cheshire cat. The executioner said, “..you couldn’t cut off a head unless there was a body to cut it off from..”

Alice and Duchess “Take care of the sense, and the sounds will take care of themselves.’ ””

Gryphon was lying fast asleep in the sun.

Alice hears the Mock turtle’s story.

So they began solemnly dancing round and round Alice.

The Lobster quadrille.

White Rabbit blew three blasts on the trumpet,White Rabbit blew three blasts on the trumpet,

White Rabbit blew three blasts on the trumpet, and reads the accusation of stealing the tarts.

Mad Hatter is the first witness. He comes with a tea cup in one hand and bread and butter in the other.

“Td rather finish my tea,” said the © Hatter, with an anxious look at the Queen, who was reading the list of singers.

“You may go,” said the King; and the Hatter hurriedly left the court, without — even waiting to put his shoes on.

The large Alice tips the jury box sending all jurors in a panic.

“Let the jury consider their verdict,” the King said, for about the twentieth time that day.
”No, no!’ said’ the, Queen. “Sentence first —verdict afterwards.”

“Who cares for you?” said Alice, (she had grown to her full size by this time.) “You’re nothing but a pack of cards!”

At this the whole pack rose up into the air, and came flying down upon her…

Gallery June 9, 2024June 11, 2024 The Mitr

Illustrations for Alice in Wonderland – Part 1 – Lewis Carroll

From the back advertisement of Carroll’s Eight or nine wise words about letter-writing (1890) illustration by John Tenniel.

Alice’s Adventures in Wonderland by Lewis Carroll (C. L. Dodgson) first published in 1865 might be one of the better known books in the world. There are several editions of it, though the text content is more or less the same, the illustrations are varied. The most famous of Alice’s illustrations are by John Tenniel. Tenniel did the 42 illustrations in the first edition and these same illustrations are found in most later editions. This series of posts is an attempt to create a collection of various illustrations for Alice in Wonderland from middle of nineteenth century. For an in-depth analysis of Alice I highly recommend reading Martin Gardner‘s Annotated Alice, which has a lot of trivia and information about the books, the characters and the author.

Signature of Lewis Carroll from the facsimile handwritten draft.

All images in public domain unless mentioned otherwise.

In this post, we start with the hand-drawn manuscript from Carroll himself which was titled Alice’s Adventures Underground. Most of the illustrations that were done later follow these pen-drawn ones in content.

A treasured early manuscript version of one of the most famous and enduring children’s stories, Alice’s Adventures in Wonderland c. 1864. Link Originally from the British Museum

Original cover of Alice’s Adventures under Ground

The facsimile version contains 40 illustrations. These illustrations were then refined by Tenniel in his woodcuts for the first edition of the book. These pen drawn crude illustrations are also templates for most of the other drawings for Alice’s books.

Alice was beginning to get very tired of sitting by her sister on the bank and having nothing to do

Alice finds a small door behind a curtain

Curioser and Curioser, now I am opening like the largest telescope that ever was!

Alice meets the rabbit again and startles it

Alice meets the mouse in the pool.

Alice led the way and the whole curious party swam ashore.

Alice has a long argument with a lory.

On various pretexts, they (birds) all moved off, and Alice was soon left alone.

Rabbit orders Alice to fetch gloves and nosegay!

Alice finds another bottle and drinks it!

..and grows in size

…till she is filling the entire room..

Alice’s hand comes out of the window of the house.

Alice kicks Bill, the green lizard, out of the chimney.

Alice meets the giant puppy.

Father William and his son.

Alice eats a mushroom and her chin is stuck to her foot!

Then she eats more and her neck shoots through the trees!

“Serpent!” A pigeon calls Alice.

Alice is of the right size and wants to go to the beautiful garden via the door in the tree.

Cards are painting white roses red in the garden.

The king and queen of hearts arrive with a knave carrying the crown in the cushion.

The curious croquet game.

Alice tries to play the croquet game with a live ostrich as a mallet and a live hedgehog as the croquet-ball.

The gryphon laid fast asleep in the Sun.

The Mock turtle tells his story.

The mock turtle and the gryphon in a tangle.

Mock turtle and gryphon sing and dance around Alice.

Sentencing of the knave of hearts for stealing of tarts.

“No!” said the Queen, “first the sentence, and then the evidence!”

Alice

April 14, 2024 The Mitr

How Many Fridays Are There in February?

Question

What is the greatest and least number of Fridays in February?

Answer

The usual answer is that the greatest number is five — the least, four. Without question, it is true that if in a leap year February 1 falls on a Friday, the 29th will also be Friday, giving five Fridays altogether.

However, it is possible to reckon double the number of Fridays in the month of February alone. Imagine a ship plying between Siberia and Alaska and leaving the Asiatic shore regularly every Friday. How many Fridays will its skipper count in a leap-year February of which the 1st is a Friday? Since he crosses the date line from west to east and does so on a Friday, he will reckon two Fridays every week; thus adding up to 10 Fridays in all. On the contrary, the skipper of a ship leaving Alaska every Thursday and heading for Siberia will “lose” Friday in his day reckoning, with the result that he won’t have a single Friday in the whole month.

So the correct answer is that the greatest number of possible Fridays in February is 10, and the least – nil.

From Astronomy for Entertainment – Yakov Perelman

December 21, 2023 The Mitr

Stellar Exploratory Data Analysis or How to create the HR Diagram with R

I recently have started to refresh my skills with R programming language. I am doing the Harvard Course on Data Science on EdX. I am using R Studio for doing all the exercises. In the second part of the course, Visualisation, which is an area of research interest for me, there is an exercise on stars dataset. But this exercise was available only to those who were crediting the course. Since I was not crediting, but only auditing I left the exercise as it is. But after a week or so I looked at the stars dataset. And thought I should do some explorations on this. For this we have to load the R package dslabs specially designed for this course. This post is detailing the exploratory data analysis with this dataset. (Disclaimer: I have used help from ChatGPT in writing this post for both content and code.)

> library(dslabs)

Once this is loaded, we load the stars dataset

data(stars)

Structure of the dataset

To understand what is the data contained in this data set and how is it structured we can use several ways. The head(stars) command will give use first few lines of the data set.

> head(stars) star magnitude temp type 1 Sun 4.8 5840 G 2 SiriusA 1.4 9620 A 3 Canopus -3.1 7400 F 4 Arcturus -0.4 4590 K 5 AlphaCentauriA 4.3 5840 G 6 Vega 0.5 9900 A

While the tail(stars) gives last few lines of the data set

tail(stars) star magnitude temp type 91 *40EridaniA 6.0 4900 K 92 *40EridaniB 11.1 10000 DA 93 *40EridaniC 12.8 2940 M 94 *70OphiuchiA 5.8 4950 K 95 *70OphiuchiB 7.5 3870 K 96 EVLacertae 11.7 2800 M

To understand structure further we can use the str(stars) command

> str(stars) 'data.frame': 96 obs. of 4 variables: $ star : Factor w/ 95 levels "*40EridaniA",..: 87 85 48 38 33 92 49 79 77 47 ... $ magnitude: num 4.8 1.4 -3.1 -0.4 4.3 0.5 -0.6 -7.2 2.6 -5.7 ... $ temp : int 5840 9620 7400 4590 5840 9900 5150 12140 6580 3200 ... $ type : chr "G" "A" "F" "K" ...

In RStudio we can also see the data with View(Stars) function in a much nicer (tabular) way. It opens up the data in another frame as shown below.

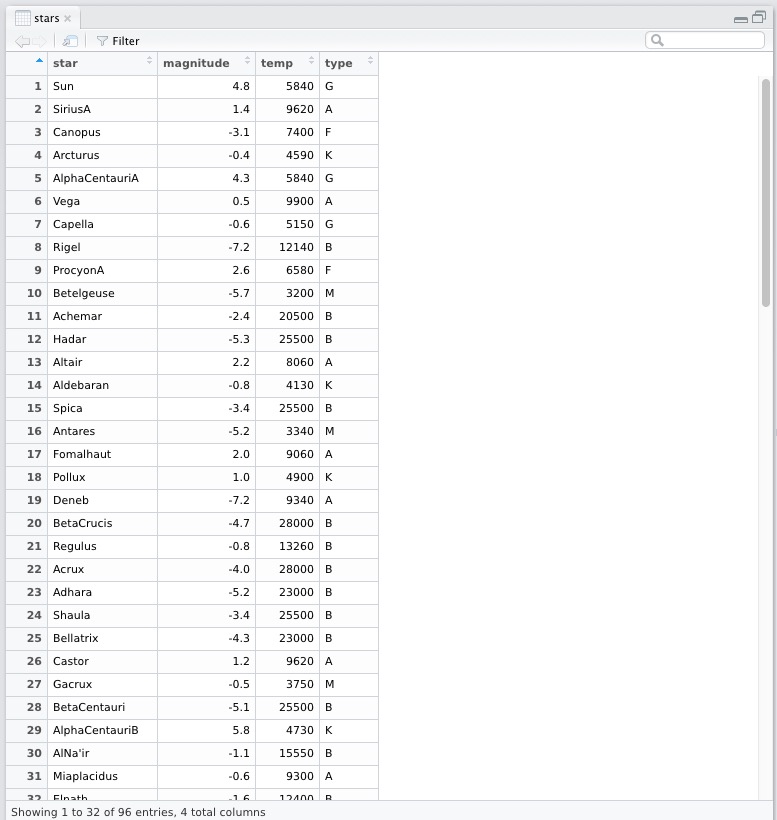
Thus we see that it has 96 observations with four variables, namely star, magnitude, temp and type. The str(stars) command also tells use the datatype of the columns, they are all different: factor, num, int, chr. Let us understand what each of the column represents.

Name of stars

The star variable has the names of the stars as seen in the table above. Many of the names are of ancient and mythological origins, while some are modern. Most are of Arabic origin, while few are from Latin. Have a look at Star Lore of All Ages by William Olcott to know some of the mythologies associated with these names. Typically the alphabets after the star names indicate them being part of a stellar system, for example Alpha Centauri is a triple star system. The nomenclature is such that A represents the brightest member of the system, B the second brightest and so on. Also notice that some names have Greek pre-fixes, as in the case of of Alpha Centauri. This Greek letter scheme was introduced by Bayer in 1603 and is known as Bayer Designation. The Greek letters denote the visual magnitude or brightness (we will come to the meaning of this next) of the stars in a given constellation. So Alpha Centuari would mean the brightest star in the Centaurus constellation. Before invention of the telescope the number of stars that are observable were limited by the limits of human visual magnitude which is about +6. With invention of telescope and their continuous evolution with increasing light gathering power, we discovered more and more stars. Galileo is the first one to view new stars and publish them in his Sidereal Messenger. He shows us that seen through the telescope, there are many more stars in the Pleiades constellation than can be seen via naked eyes (~+6 to max +7 with about 4200 stars possibly visible).

Soon, so many new stars were discovered that it was not possible to name them all. So coding of the names begun. The large telescopes which were constructed would do a sweep of the sky using big and powerful lenses and would create catalogue of stars. Some of the names in the data set indicate these data sets, for example HD denotes Henry Draper Catalogue.

Magnitudes of stars

Now let us look at the other three columns present us with observations of these stars. Let us understand what they mean. The second column represents magnitude of the stars. The stellar magnitude is of two types: apparent and absolute. The apparent magnitude is a measure of the brightness of the star and depends on its actual brightness, distance from us and any loss of the brightness due to intervening media. The magnitude scale was devised by Claudius Ptolemy in second century. The first magnitude stars were the brightest in the sky with sixth being the dimmest. The modern scale follows this classification and has made it mathematical. The scale is reverse logarithmic, meaning that lower the magnitude, brighter is the object. A magnitude difference of 1.0 corresponds to a brightness ratio of $ \sqrt[5]{100} $ or about 2.512. Now if you are wondering why the magnitude scale is logarithmic, the answer lies in the physiology of our visual system. As with the auditory system, our visual system is not linear but logarithmic. What this means is that if we perceive an object to be of double brightness of another object, then their actual brightness (as measured by a photometer) are about 2.5. This fact is encapsulated well in the Weber-Fechnar law. The apparent magnitude of the Sun is about -26.7, it is after all the brightest object in the sky for us. Venus, when it is brightest is about -4.9. The apparent magnitude of Neptune is +7.7 which explains why it was undiscovered till the invention of the telescope.

But looking at the table about the very first entry lists Sun’s magnitude as +4.8. This is because the dataset contains the absolute magnitude and not the apparent magnitude. Absolute magnitude is defined as “apparent magnitude that the object would have if it were viewed from a distance of exactly 10 parsecs (32.6 light-years), without dimming by interstellar matter and cosmic dust.” As we know, the brightness of an object is inversely proportional to square of the distance (inverse square law). Due to this fact very bright objects can appear very dim if they are very far away, and vice versa. Thus if we place the Sun at a distance of about 32.6 light years it will be not-so-bright and will be an “average” star with magnitude +4.8. The difference in these two magnitudes is -31.57 and this translates to huge brightness difference of 3.839 $\times$ 10¹². And of course this definition does not take into account the interstellar matter which further dims the stars. Thus to find the absolute magnitude of the stars we also need to know their distance. This is possible for some nearby stars for which the parallax has been detected. But for a vast majority of stars, the parallax is too small to be detected because they are too faraway. The distance measure parsec we saw earlier is defined on basis of parallax, one parsec is the distance at which 1 AU (astronomical unit: distance between Earth and Sun) subtends an angle of one arcsecond or 1/3600 of a degree.

Thus finding distance to the stars is crucial if we want to know their actual magnitudes. For finding the cosmic distances various techniques are used, we will not go into their details. But for our current purpose, we know that the stars dataset has absolute magnitudes of stars. The range of magnitudes in the dataset is

> range(stars$magnitude) [1] -8 17

Thus stars in the dataset have a difference of 25 magnitudes, that is a brightness ratio of 10⁵! Which are these brightest and dimmest stars? And how many stars of each magnitude are there in the data set? We can answer these type of questions with simple queries to our dataset. For starters let us find out the brightest and dimmest stars in the dataset. Each row in the dataset has an index, which is the first column in the table from RStudio above. Thus if we were to write:

> stars[1]

it will give us all the entries of the first column,

star 1 Sun 2 SiriusA 3 Canopus 4 Arcturus 5 AlphaCentauriA 6 Vega 7 Capella 8 Rigel 9 ProcyonA 10 Betelgeuse ... ...

But if we want only a single row, instead of a column, we have to tell that by keeping a , in the index 1. Thus for the first row we write
> stars[1,] > star magnitude temp type 1 Sun 4.8 5840 G

Thus to find the brightest or dimmest star we will have to find its index and then we can find its name from the corresponding column. So how do we do that? For this we have functions which.max and which.min, we use them thus:

> which.max(stars$magnitude) [1] 76

We feed this to the dataset and get
> stars[76,] star magnitude temp type 76 G51-I5 17 2500 M

This can also be done in a single line

> stars[which.min(stars$magnitude), ] star magnitude temp type 45 DeltaCanisMajoris -8 6100 F

Now let us check the distribution of these magnitudes. The simplest way to do this is to create a histogram using the hist function.

hist(stars$magnitude)

This gives the following output

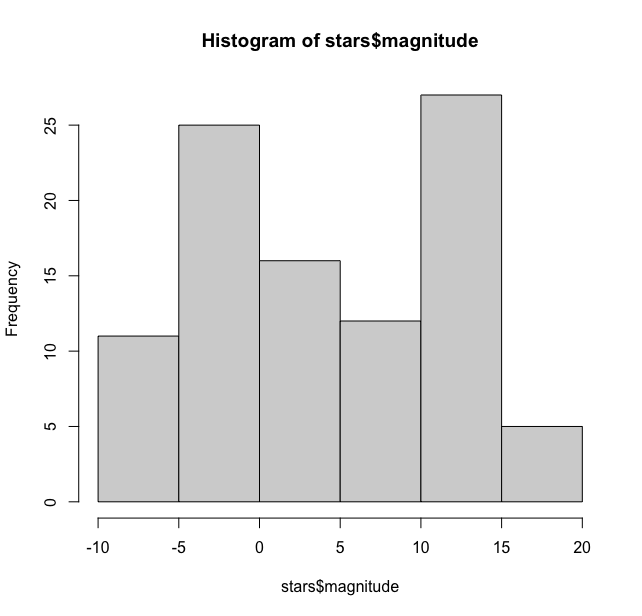
As we can see it has by default binned the magnitudes in bins of 5 units and the distribution here is bimodal with one peak between -5 and 0 and another peak between 10 and 15. We can tweak the width of the bars to get a much finer picture of the distribution. For this hist function has option to add breaks manually. We have used the seq function here ranging from -10 to 20 in steps of 1.

> hist(stars$magnitude, breaks = seq(-10, 20, by = 1))

And this gives us:

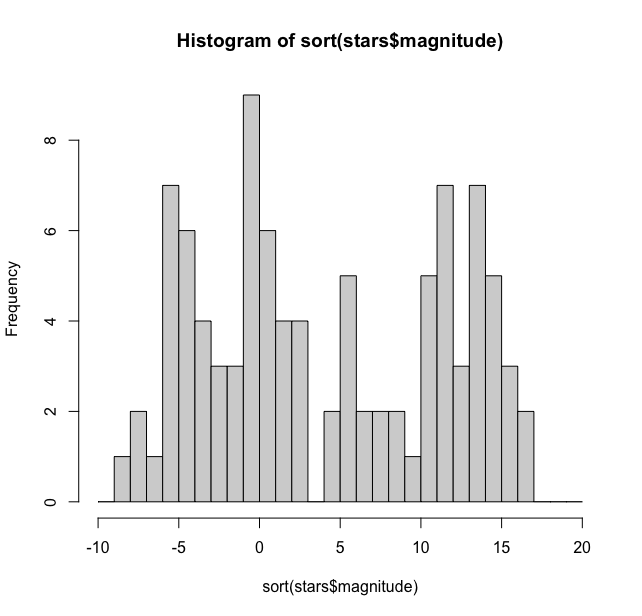
Thus we see that the maximum number of stars (9) are at -1 magnitude and three magnitudes have one star each while +3 magnitude doesn’t have any stars. This histogram could be made more reader friendly if we can add the count on the bars. For this we need to get some coordinates and numbers. We first get the counts

mag_data <- hist(stars$magnitude, breaks = seq(-10,20, 1), plot = FALSE)

This will give us the actual number of counts

> [1] 0 1 2 1 7 6 4 3 3 9 6 4 4 0 2 5 2 2 2 1 5 7 3 7 5 3 2 0 0 0

Now to place them at the middle of the bars of histogram we need midpoints of the bars, we use mag_data$mids to find them and mag_data_counts for the count for labels.

> text(mag_data$mids, mag_data$counts, labels = mag_data$counts, pos = 3, cex = 0.8, col = "black")

To get the desired graph

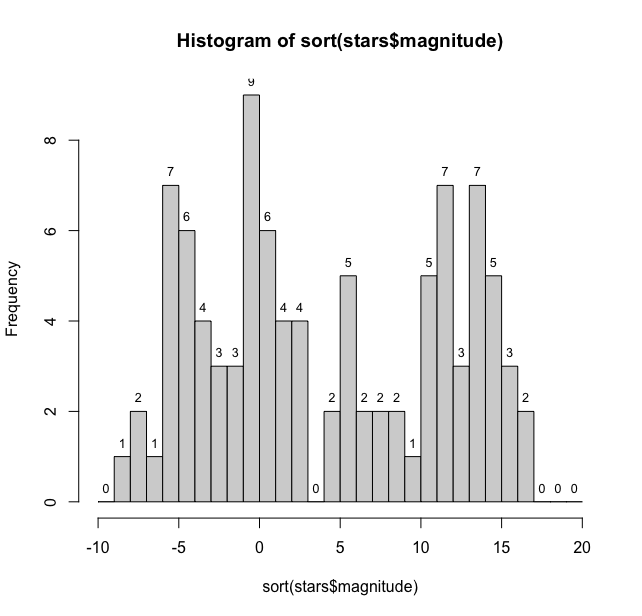
Thus we have a fairly large distribution of stellar magnitudes.

Now if we ask ourselves this question How many stars in this dataset are visible to the naked eye? What can we say? We know that limiting magnitude for naked eye is +6. So, a simple query should suffice:

count(stars %>% filter(magnitude <= 6)) n 1 57

(Here we have used the pipe function %>% to pass on data from one argument to another from the dplyr pacakge. This query shows that we have 57 stars which have magnitude less than or equal to 6. Hence these many should be visible… But wait it is the absolute magnitude that we have in this dataset, so this question itself cannot be answered unless we have the apparent magnitudes of the stars. Though computationally correct, this answer has no meaning as it is cannot be treated same as the one with apparent magnitude which we experience while watching the stars.

Temperature of Stars

The third column in the data set is the temp or the temperature. Now, at one point in the history of astronomy people believed that we would never be able to understand the structure or the content of the stars. But the invention of spectroscopy as a discipline and its application to astronomy made this possible. With the spectroscope applied to the end of the telescope (astronomical spectroscopy), we could now understand the composition of the stars, their speed and their temperature. The information for the composition came from the various emission and absorption lines in the spectra of the stars, which were then compared with similar lines produced in the laboratory by heating various elements. Helium was first discovered in this manner: first in the spectrum of the Sun and then in the laboratory. For detailed story of stellar spectroscopy one can see the book Astronomical Spectrographs and Their History by John Hearnshaw. Though an exact understanding of the origin of the spectral line came only after the advent of quantum mechanics in early part of 20th century.

But the spectrum also tells us about the surface temperature of the stars. How this is so? For this we need to invoke one of the fundamental ideas in physics: the blackbody radiation. Now if we find the intensity of radiation from a body at different wavelengths (or frequencies) we get a curve. This curve is typical and for different temperatures we get unique curves (they don’t intersect). Of course this is true for an ideal blackbody which is an idealized opaque, non-reflective body. Stellar spectrum is like that of an ideal blackbody, this continuous spectrum is punctuated with absorption and emission lines as shown in the book cover above.

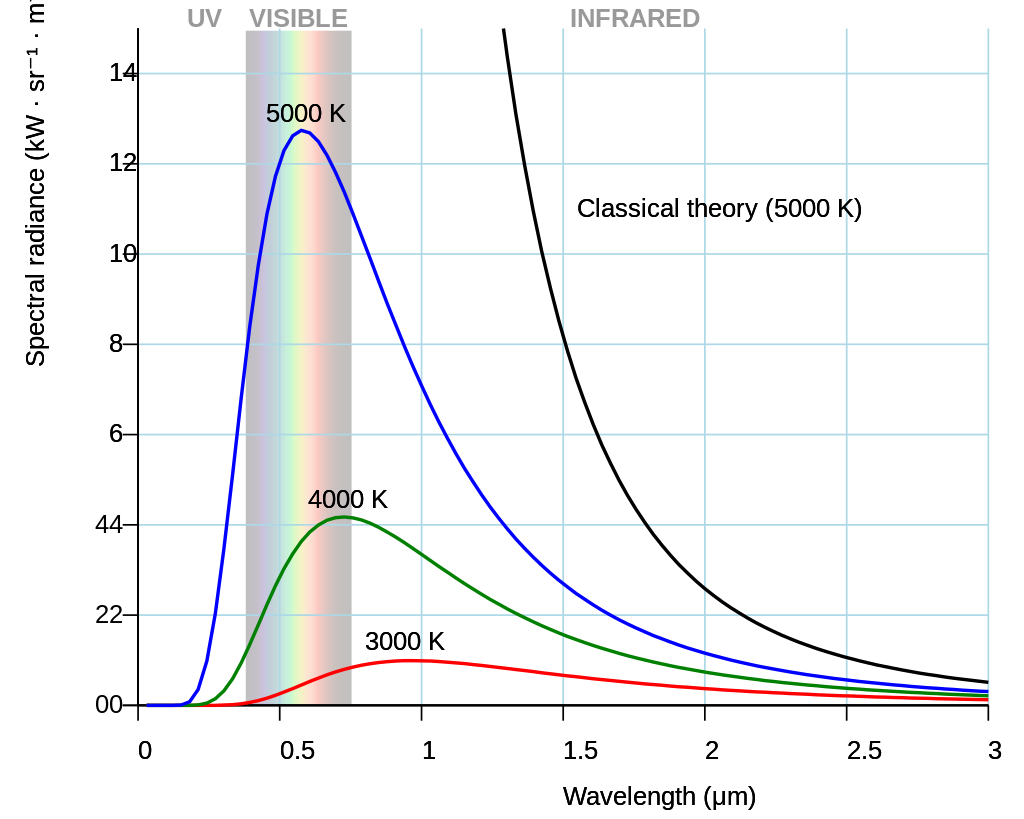
The frequency or wavelength at which the radiation has maximum intensity (brightness/luminosity) is related to the temperature of the body, typical curves are shown as above. Stars behave almost as ideal black bodies. Notice that as the temperature of the body increases the peak radiation wavelength increases (frequency is reduced) as shown in the diagram above. These relationships are given by the formula

$$
L = 4 \pi R^{2} \sigma T^{4}
$$

where $L$ is the luminosity, $R$ is the radius, $\sigma$ is Stephan’s constant and $T$ is the temperature. This equation tells us that $L$ is much more dependent on the $T$, so hotter stars would be more brighter.

It was failure of the classical ideas of radiation and thermodynamics to explain the nature of blackbody radiation that led to formulation of quantum mechanics by Max Planck in the form of Planck’s law for quantisation of energy. For a detailed look at the history of this path breaking episode in history of science one of the classics is Thomas Kuhn’s Black-Body Theory and the Quantum Discontinuity, 1894—1912.

That is to say hotter bodies have shorter peak frequencies. In other words, blue stars are hotter than the red ones. (Our hot and cold symbolic colours on the plumbing peripherals needs to change: we have it completely wrong!) Thus the spectrum of the stars gives as its absolute temperature, along with all other information that we can obtain from the stars. The spectrum is our only source of information for stars. This is what is represented in the third column of our data. For our dataset the range of stellar temperatures we have a wide range of temperatures.

range(stars$temp) [1] 2500 33600

Let us explore this column a bit. If we plot a histogram with default options we get:

> hist(stars$temp)

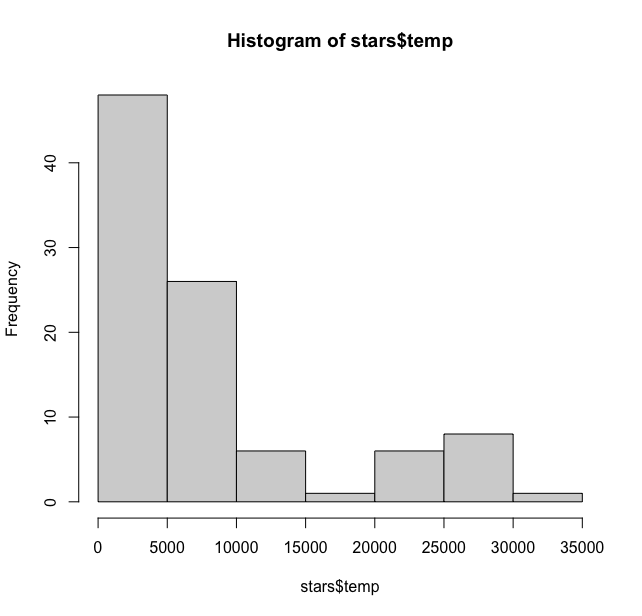
This is showing maximum stars have a temperature below 10000. We can bin at 1000 and add labels to get a much better sense. Which star has 0 temperature??

hist(stars$temp, breaks = seq(0,35000, 1000)) > temp_data <- hist(stars$temp, breaks = seq(0,35000, 1000), plot = FALSE) > text(temp_data$mids, temp_data$counts, labels = temp_data$counts, pos = 3, cex = 0.8, col = "black")

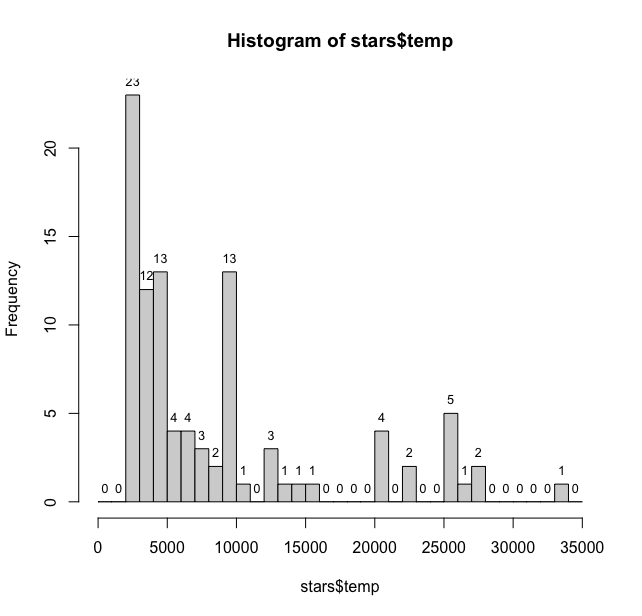
This plot gives us much better sense of the distribution of stellar temperatures. With most of the temperatures being in 2000-3000 degrees Kelvin range. The table() function also provides useful information about distribution of temperatures in the column.

> table(stars$temp)

2500 2670 2800 2940 3070 3200 3340 3480 3750 3870 4130 4590 1 10 7 5 1 3 4 1 1 2 3 3 4730 4900 4950 5150 5840 6100 6580 6600 7400 7700 8060 9060 1 5 1 2 2 2 1 1 2 1 2 1 9300 9340 9620 9700 9900 10000 11000 12140 12400 13000 13260 14800 1 2 3 1 4 1 1 1 1 1 1 1 15550 20500 23000 25500 26950 28000 33600 1 4 2 5 1 2 1

While the summary() function provides the basic statistics:

> summary(stars$temp) Min. 1st Qu. Median Mean 3rd Qu. Max. 2500 3168 5050 8752 9900 33600

Type of Stars

The fourth and final column of our data is type. This category of data is again based on the spectral data of stars and is type of spectral classification of stars. “The spectral class of a star is a short code primarily summarizing the ionization state, giving an objective measure of the photosphere’s temperature. ” The categories of the type of stars and their physical properties are summarised in the table below. The type of stars and their temperature is related, with “O” type stars being the hottest, while “M” type stars are the coolest. The Sun is an average “G” type star.

There are several mnemonics that can help one remember the ordering of the stars in this classification. One that I still remember from by Astrophysics class is Oh Be A Fine Girl/Guy Kiss Me Right Now. Also notice that this “type” classification is also related to size of the stars in terms of solar radius.

In our dataset, we can see what type of stars we have by

> stars$type [1] "G" "A" "F" "K" "G" "A" "G" "B" "F" "M" "B" "B" "A" "K" [15] "B" "M" "A" "K" "A" "B" "B" "B" "B" "B" "B" "A" "M" "B" [29] "K" "B" "A" "B" "B" "F" "O" "K" "A" "B" "B" "F" "K" "B" [43] "B" "K" "F" "A" "A" "F" "B" "A" "M" "K" "M" "M" "M" "M" [57] "M" "A" "DA" "M" "M" "K" "M" "M" "M" "M" "K" "K" "K" "M" [71] "M" "G" "F" "DF" "M" "M" "M" "M" "K" "M" "M" "M" "M" "M" [85] "M" "DB" "M" "M" "A" "M" "K" "DA" "M" "K" "K" "M"

Our Sun is G-type star in this classification (first entry). If we use the table() function on this column we get the frequency of each type of star in the dataset.

> table(stars$type)

A B DA DB DF F G K M O
13 19 2 1 1 7 4 16 32 1

And to see a barplot of this table we will use ggplot2() package. Load the package using library using library(ggplot2) and then

> stars %>% ggplot(aes(type)) + geom_bar() + geom_text(stat = "count", aes(label = after_stat(count)), vjust = -0.5, size = 4)

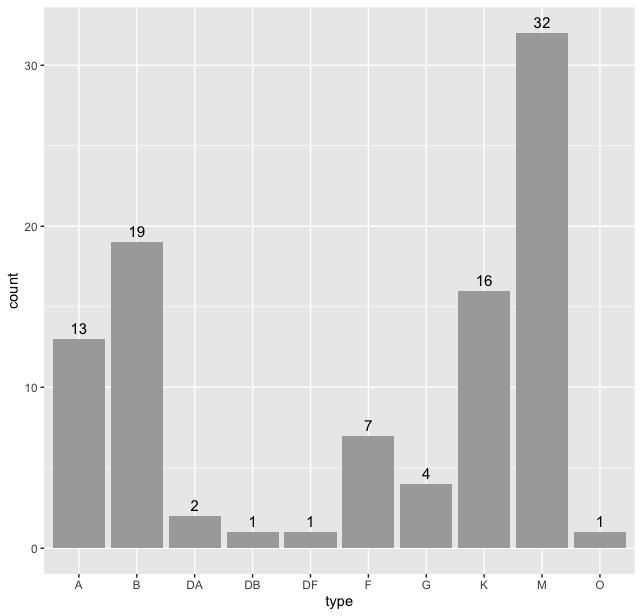
Thus we see that “M” type stars are the maximum in our dataset. But we can do better, we can sort this data according the frequency of the types. For this we use the code:

> type_count <- table(stars$type) > # count the frequencies > sorted_type <- names(sort(type_count)) > # sort them > stars$type <- factor(stars$type, levels = sorted_type) > # reorder them with levels and plot them > stars %>% ggplot(aes(type)) + geom_bar(fill = "darkgray") + geom_text(stat = "count", aes(label = after_stat(count)), vjust = -0.5, size = 4)

And we get

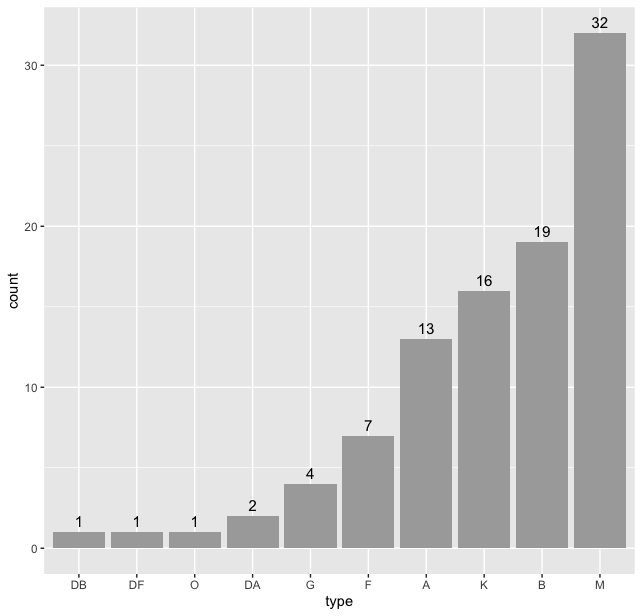
To plot HR Diagram

Now, given my training in astronomy and astrophysics, the first reaction that came to my mind after seeing this data was this is the data for the HR Diagram! The HR diagram presents us with the fundamental relationship of types and temperature of stars. This was an crucial step in understanding stellar evolution. The intials HR stand for the two astronomers who independently found this relationship: The diagram was created independently in 1911 by Ejnar Hertzsprung and by Henry Norris Russell in 1913.

By early part of 20th century several star catalogues had been around, but nothing stellar evolution or structure was known. The stellar spectrographs revealed what elements were present in the stars, but the energy source of the stars was still an unresolved question. Classical physics had no answer to this fundamental question about how stars were able to create so much energy (for example, see Stars A Very Short Introduction by James Kaler on the idea that charcoal powers the Sun by Lord Kelvin). Added to this was the age of the stars, from geological data and idea of geological deep time, the Sun was estimated to be 4 billion years old as was the Earth. So stars had been producing so much energy for such a long time! But that is not the point of this post, the HR diagram definitely helped the astronomers think about the idea that stars might not be static but evolve in time. The International Astronomical Union conducted a special symposium titled The HR Diagram in 1977. The proceedings of the symposium have several articles of interest on the history of creation and interpretation of the HR Diagram.

I think it was but natural that astronomers tried to find correlations between various properties of thousands of stars in these catalogues. And when they did they find a (co-)relationship between them. The HR diagram exists in many versions, but the basic idea is to plot the absolute magnitude and temperature (or colour index). Let us plot these two to see the co-relation, for this we again use the ggplot2() pacakge and its scatterplot function geom_point().

> stars %>% ggplot(aes(temp, magnitude)) + geom_point()

This gives us the basic plot of HR diagram.

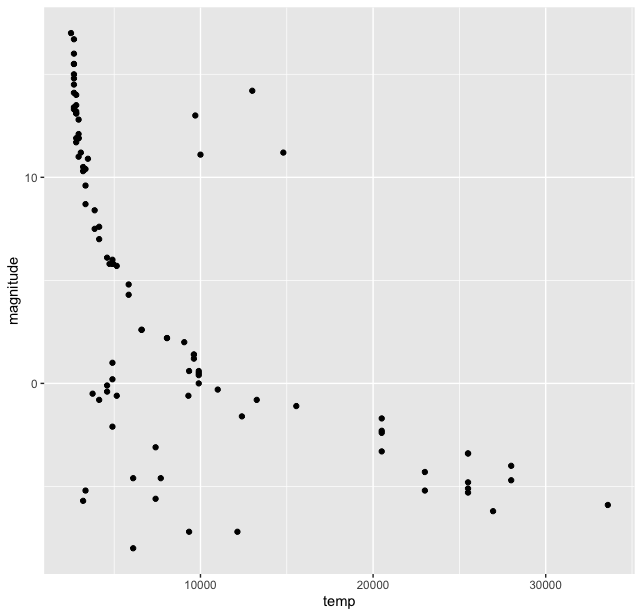
Immediately we can see that the stars are not randomly scattered on this plot, but are grouped in clusters. And most of them lie in a “band”. Though there are outliers at the lower temperature and magnitude range and high magnitude and temperature around 10-15 thousand range. We see that most stars lie in a band which is called the “Main Sequence”. We can try to fit a function here in this plot using some options in the ggplot() library, we use geom_smooth() function for this and get:

stars %>% ggplot(aes(temp, magnitude)) + geom_point() + geom_smooth( se = FALSE, color = “red”)

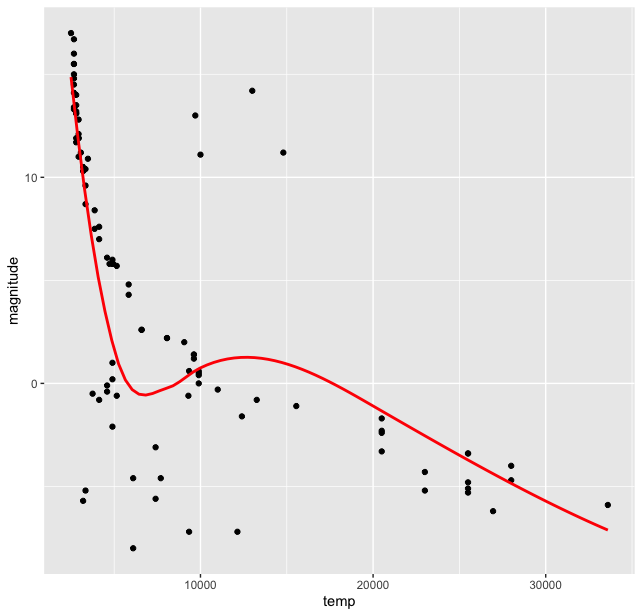
Of course this smooth curve is a very crude (perhaps wrong?) approximation of the data, but it certainly points us towards some sort of correlation between the two quantities for most of the stars. But wait, we have another categorical variable in our dataset, the type of stars. How are the different types of stars distributed on this curve? For this we introduce type variable in the aesthetics argument of ggplot() to colour the stars on our plot according to this category:

> stars %>% ggplot(aes(temp, magnitude, color = type)) + geom_smooth( se = FALSE, color = "red") + geom_point()

This produces the plot

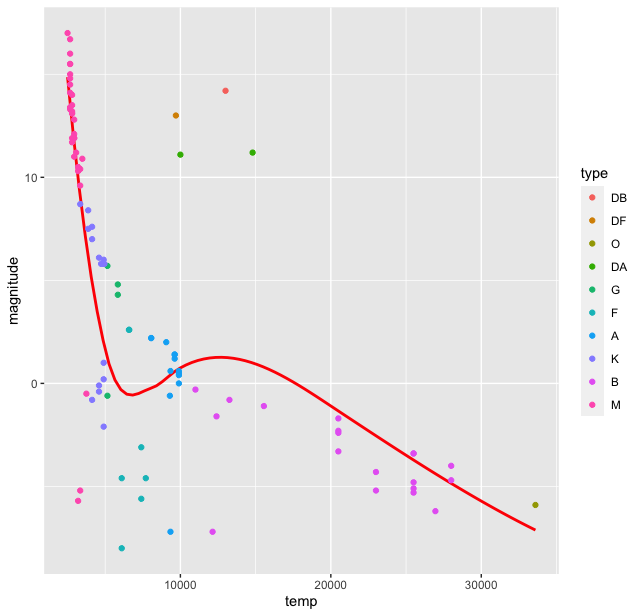
Thus we see there is a grouping of stars by the type. Of course the colours in the palette here are not the true representatives of the star colours. The HR diagram was first published around 1911-13, when quantum mechanics was in its nascent stages. The ideas of Rutherford’s model were still extant and was just out. The fact that this diagram indicated a relationship between the magnitude and temperature, led to thinking about stellar structure itself and its ways of producing energy with fundamentally new ideas about matter and energy from quantum mechanics and their transformation from relativistic physics. But that is a story in future. For now, let us come to our HR diagram. From the dataset we have one more variable, the star name which could be used in this plot. We can name all the stars in the plot (there are only 96). For this we use the geom_text() function in ggplot()

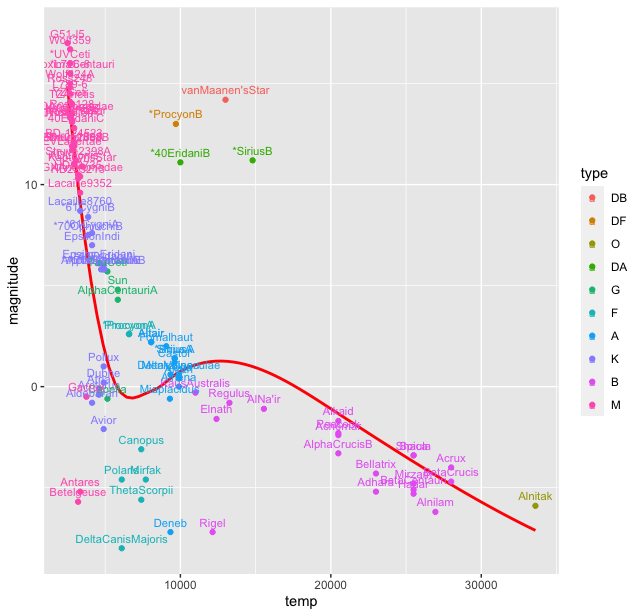
> stars %>% ggplot(aes(temp, magnitude, color = type), label = star) + geom_smooth( se = FALSE, color = "red") + geom_point() + geom_text((aes( label = star)), nudge_y = 0.5, size = 3)

This produces a rather messy plot, where most of the starnames are on top of each other and not readable:

To overcome this clutter we use another package ggrepel() with the following code:

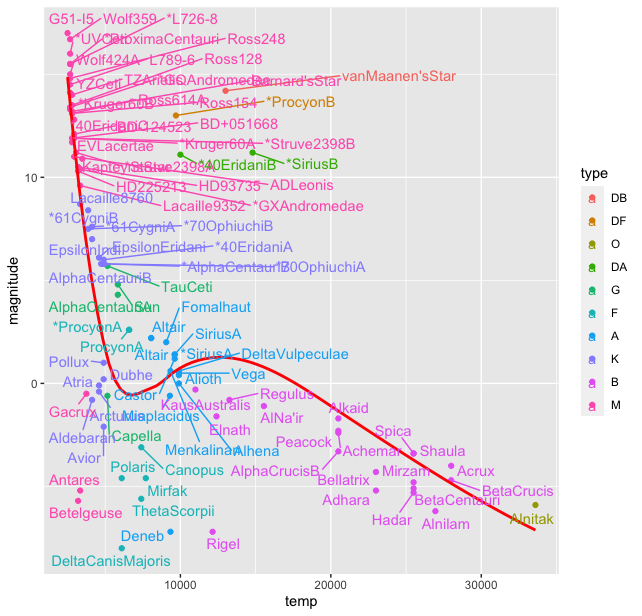
> stars %>% ggplot(aes(temp, magnitude, color = type), label = star) + geom_smooth( se = FALSE, color = "red") + geom_text_repel(aes(label = star))

This produces the plot with the warning "Warning message: ggrepel: 13 unlabeled data points (too many overlaps). Consider increasing max.overlaps ". To overcome this we increase the max.overlaps to 50.

> stars %>% ggplot(aes(temp, magnitude, color = type), label = star) + geom_point() + geom_smooth( se = FALSE, color = "red") + geom_text_repel(aes(label = star), max.overlaps = 50)

This still appears cluttered a bit, scaling the plot while exporting gives this plot, though one would need to zoom in to read the labels.

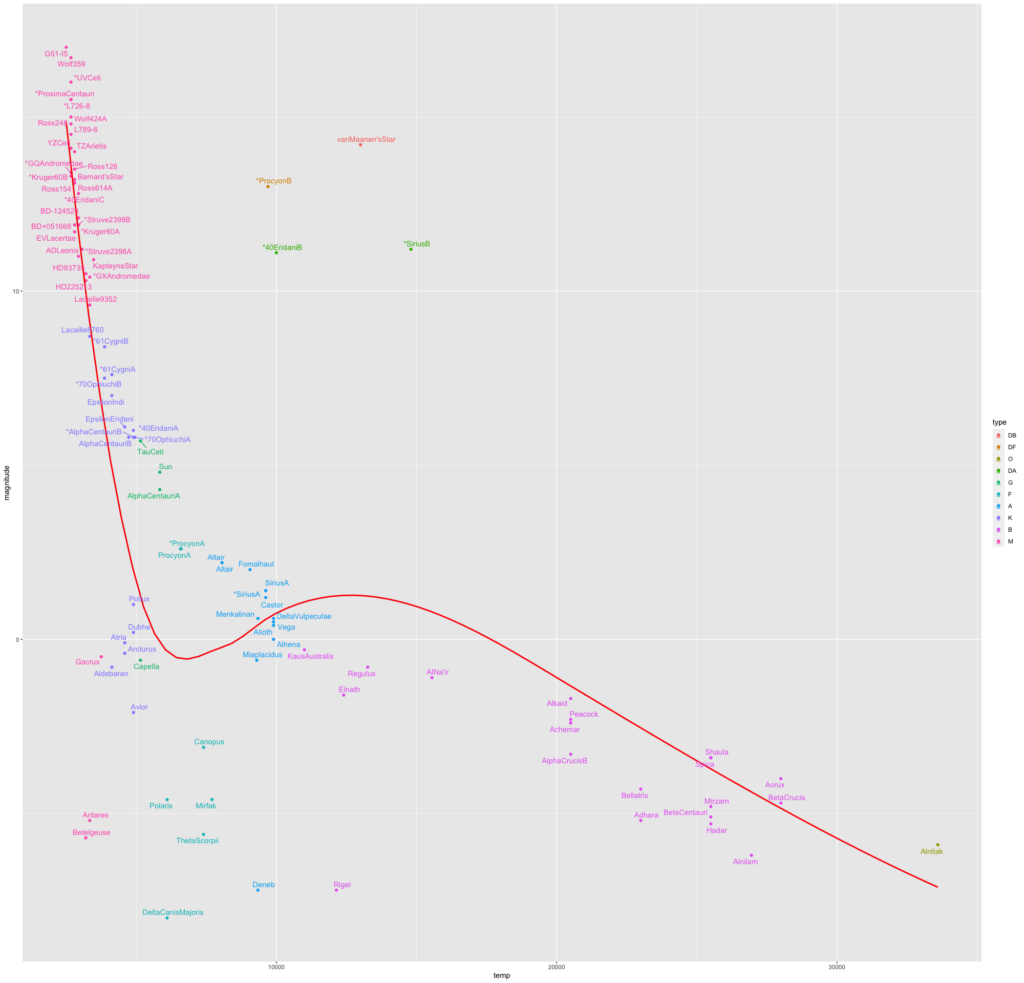
Of course with a different data set, with larger number and type of stars we would see slightly different clustering, but the general pattern is the same.

We thus see that starting from the basic data wrangling we can generate one of the most important diagrams in astrophysics. I learned a lot of R in the process of creating this diagram. Next task is to

November 18, 2023November 19, 2023 The Mitr

How big is the shadow of the Earth?

The Sun is our ultimate light source on Earth. The side of the Earth facing the Sun is bathed in sunlight, due to our rotation this side changes continuously. The side which faces the Sun has the day, and the other side is the night, in the shadow of the entire Earth. The sun being an extended source (and not a point source), the Earth’s shadow had both umbra and penumbra. Umbra is the region where no light falls, while penumbra is a region where some light falls. In case of an extended source like the Sun, this would mean that light from some part of the Sun does fall in the penumbra. Occasionally, when the Moon falls in this shadow we get the lunar eclipse. Sometimes it is total lunar eclipse, while many other times it is partial lunar eclipse. Total lunar eclipse occurs when the Moon falls in the umbra, while partial one occurs when it is in penumbra. On the other hand, when the Moon is between the Earth and the Sun, we get a solar eclipse. The places where the umbra of the Moon’s shadow falls, we get total solar eclipse, which is a narrow path on the surface of the Earth, and places where the penumbra falls a partial solar eclipse is visible. But how big is this shadow? How long is it? How big is the umbra and how big is the penumbra? We will do some rough calculations, to estimate these answers and some more to understand the phenomena of eclipses.

We will start with a reasonable assumption that both the Sun and the Earth as spheres. The radii of the Sun, the Earth and the Moon, and the respective distances between them are known. The Sun-Earth-Moon system being a dynamic one, the distances change depending on the configurations, but we can assume average distances for our purpose.

[The image above is interactive, move the points to see the changes. This construction is not to scale!. The simulation was created with Cinderella ]

The diameter of the Earth is approximately 12,742 kilometers, and the diameter of the Sun is about 1,391,000 kilometers, hence the ratio is about 109, while the distance between the Sun and the Earth is about 149 million kilometers. A couple of illustrations depicting it on the correct scale.

The Sun’s (with center A) diameter is represented by DF, while EG represents Earth’s (with center C) diameter. We connect the centers of Earth and Sun. The umbra will be limited in extent in the cone with base EG and height HC, while the penumbra is infinite in extent expanding from EG to infinity. The region from umbra to penumbra changes in intensity gradually. If we take a projection of the system on a plane bisecting the spheres, we get two similar triangles HDF and HEG. We have made an assumption that our properties of similar triangles from Euclidean geometry are valid here.

In the schematic diagram above (not to scale) the umbra of the Earth terminates at point H. Point H is the point which when extended gives tangents to both the circles. (How do we find a point which gives tangents to both the circles? Is this point unique?). Now by simple ratio of similar triangles, we get

$$
\frac{DF}{EG} = \frac{HA}{HC} = \frac{HC+AC}{HC}
$$

Therefore,

$$
HC = \frac{AC}{DF/EG -1}
$$

Now, $DF/EG = 109$, and $AC$ = 149 million km, substituting the values we get the length of the umbra $HC \approx$ 1.37 million km. The Moon, which is at an average distance of 384,400 kilometers, sometimes falls in this umbra, we get a total lunar eclipse. The composite image of different phases of a total lunar eclipse below depicts this beautifully. One can “see” the round shape of Earth’s umbra in the central three images of the Moon (red coloured) when it is completely in the umbra of the Earth (Why is it red?).

When only a part of umbra falls on the moon we get a partial lunar eclipse as shown below. Only a part of Earth’s umbra is on the Moon.

So if the moon was a bit further away, lets say at 500,000 km, we would not get a total solar eclipse. Due to a tilt in Moon’s orbit not every new moon is an eclipse meaning that the Moon is outside both the umbra and the penumbra.

The observations of the lunar eclipse can also help us estimate the diameter of the Moon.

Similar principle applies (though the numbers change) for solar eclipses, when the Moon is between the Earth and the Sun. In case of the Moon, ratio of diameter of the Sun and the Moon is about 400. With the distance between them approximately equal to the distance between Earth and the Sun. Hence the length of the umbra using the above formula is 0.37 million km or about 370,000 km. This makes the total eclipse visible on a small region of Earth and is not extended, even the penumbra is not large (How wide is the umbra and the penumbra of the moon on the surface of the Earth?).

When only penumbra is falling on a given region, we get the partial solar eclipse.

You can explore when solar eclipse will occur in your area (or has occurred) using the Solar Eclipse Explorer.

This is how the umbra of the Moon looks like from space.

And same thing would happen to a globe held in sunlight, its shadow would be given by the same ratio.

Thus we see that the numbers are almost matched to give us total solar eclipse, sometimes when the moon is a bit further away we may also get what is called the annular solar eclipse, in which the Sun is not covered completely by the Moon. Though the total lunar eclipses are relatively common (average twice a year) as compared to total solar eclipses (once 18 months to 2 years). Another coincidence is that the angular diameters of the Moon and the Sun are almost matched in the sky, both are about half a degree (distance/diameter ratio is about 1/110). Combined with the ratio of distances we are fortunate to get total solar eclipses.

Seeing and experiencing a total solar eclipse is an overwhelming experience even when we have an understanding about why and how it happens. More so in the past, when the Sun considered a god, went out in broad daylight. This was considered (and is still considered by many) as a bad omen. But how did the ancient people understand eclipses? There is a certain periodicity in the eclipses, which can be found out by collecting large number of observations and finding patterns in them. This was done by ancient Babylonians, who had continuous data about eclipses from several centuries. Of course sometimes the eclipse will happen in some other part of the Earth and not be visible in the given region, still it could be predicted. To be able to predict eclipses was a great power, and people who could do that became the priestly class. But the Babylonians did not have a model to explain such observations. Next stage that came up was in ancient Greece where models were developed to explain (and predict) the observations. This continues to our present age.

The discussion we have had applies in the case when the light source (in this case the Sun) is larger than the opaque object (in this case the Earth). If the the light source is smaller than the object what will happen to the umbra? It turns out that the umbra is infinite in extent. You see this effect when you get your hand close to a flame of candle and the shadow of your hand becomes ridiculously large! See what happens in the interactive simulation above.

References

James Southhall Mirrors, Prisms and Lenses (1918) Macmillan Company

Eric Rogers Physics for the Inquiring Mind (1969) Princeton

July 14, 2023 The Mitr

Remarkable Curves 1: The Straight Line and the Circle

The Straight Line and the circle

(Note: All the images are interactive, move the points around to see. Dynamic mathematics interactive web page with Cinderella )

A moving point describes a straight line when it passes from one
position to another along the shortest possible path. A straight line
can be drawn with the help of a ruler; when a pencil runs along the
edge of a ruler it leaves a trace on the paper in the form of a
straight line.

When a point moves on a surface at a constant distance from another
fixed point on the same surface it describes a circle. Because of this
property of the circle we are able to draw a circle with the help of
compasses.

The straight line and the circle are the simplest and at the same time
the most remarkable curves as far as their properties are concerned.

You are no doubt more familiar with these two curves than with
others. But you should not imagine that you know all of the most
important properties of straight lines and curves. For example, you
may not know that if the vertices of the triangles $ABC$ and $AB’C’$
lie on three straight lines intersecting at the point $S$ (Fig. 1),
the three points of intersection $M$, $K$, $L$ of the corresponding
sides of the triangles, the sides $AB$ and $A’B’$, $BC$ and $B’C’$,
and $AC$ and $A’C’$, must be collinear, that is, they lie on a single
straight line.

(Note: this image below is interactive, move the points to see the dynamic change!)

You are sure to know that a point $M$ moving in a plane equidistantly
from two fixed points, say $F_1$, and $F_2$, of the same plane, that
is, so that $MF_{1}= MF_{2}$, describes a straight line (Fig. 2).

But you might find it difficult to answer the question:

What type of curve will point $M$ describe if the distance of $M$ from
$F_1$, is a certain number of times greater than that from $F_2$ (for
instance, in Fig. 3 it is twice as great)?

The curve turns out to be a circle. Hence if the point $M$ moves in a
plane so that the distance of $M$ from one of the fixed
points. $F_{1}$ or $F_{2}$, in the same plane is always proportional
to the distance from the other fixed point, that is

$$
MF_{1} = k \times MF_{2}
$$

then $M$ describes either a straight line (when the factor of
proportionality is unity) or a circle (when the factor of
proportionality is other than unity).

This is a post to create interactive mathematics elements using Cinderella a Free Software alternative to GeoGebra which is no longer a Free Software. The files have been exported from Cinderella at html interactives)

June 29, 2023 The Mitr

Preternatural Photographs

A red bloom from Indian summer. This photo has flowers from the Canonball tree, Gulmohar and African Tulip taken by keeping them on a notebook Taken with one of the most basic cameras the Canon A800.

I got my first camera c. 2005. It was the Canon S2 with 12x optical zoom and 5 MP sensor and could support a 1 GB memory card. By today’s standards these specs look very primitive, but this is almost 18 years ago. I have taken several thousand pictures with that camera, resetting the image counter two times. About 2015 the camera sensor gave up, and they could not repair it. The camera, had super zoom for those days, but its macro function was excellent in terms of focusing very well on the macro subjects. Then I got my hands on DSLRs the Sony Alpha 350 and then finally a Nikon D300 with excellent selection of prime lenses. But this post is not about the cameras per se, but the photographs.

The magnificent flower of Epiphyllum oxypetallum (mistaken popularly as bramhakamal), taken with Canon S2.

Among all the photos that I have taken some just stand out from the rest. The light, the focus, the exposure and the framing is just perfect. I don’t know how to explain this aesthetic appeal of these photographs. But in these photos, even amongst a batch of hundreds taken in the same setting or with same subjects, some photos just come out extraordinary as compared to the rest. As a photographer you might have experienced this too.

Sophia College, Mumbai corridor, taken with Nikon D300

I am a very visual oriented person. Ever since I remember from my childhood, I have been always attracted to images and visual depictions. This is what led to me reading comics. The visual impact. Also, in my house there were always art projects my mother did such as embroidery, paintings among other things. And I was fascinated by colours and drawings. Though I am not very good at drawing, I can certainly appreciate good ones.

Water lily fields submerged near the origin of Mooi river (Taken with Motorola E6). This is one my favourite photos that I have taken.

But coming to photos, some photos make a connection with your very being, inner-self of you. I cannot explain it. But you can experience the photo at some deeper level than the perceptual one. From what I have gathered talking to other people “seeing” the same image, but this experience might be unique, as not every one feels this special connection. You have your favourite photographs, they are really powerful when they speak to you directly transcending the boundaries of space and time.

A poppy flower in a poppy field (Taken with Canon EOS 80D)

I don’t know if there is a cognitive theory that will explain this in terms of our earlier experiences with images or social interactions with media. But this connection that you feel is real and I can’t put it in exact words…

Temet Nosce

Know Thyself Too…